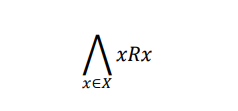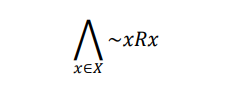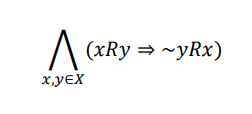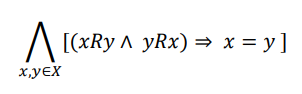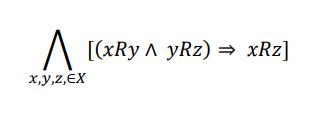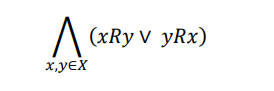All algorithms examining the relationship are presented in the form of code in C and JS.
1. Reflexivity
The relationship R defined on set X is reflexive when for every element x ∈ X, that element remains in relation with itself.
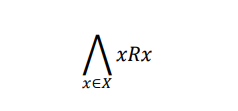
2. Irreflexivity
The relationship R defined on set X is irreflexive when no element x ∈ X is in relation with itself.
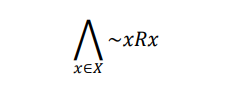
3. Symmetry
The relationship R defined on set X is symmetric when for any two elements x, y ∈ X, if x is in relation with element y, then y is also in relation with element x.
4. Asymmetry
The relationship R defined on set X is antisymmetric when for any two elements x, y ∈ X, if x is in relation with y, then y is not in relation with x.
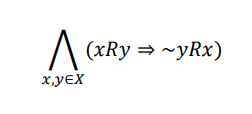
5. Antisymmetry
The relationship R defined on set X is antisymmetric if for any two elements x, y ∈ X, if x is in relation with element y and y is in relation with element x, then elements x and y are identical.
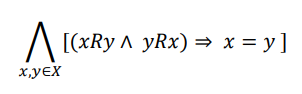
6. Transitivity
The relationship R defined on set X is transitive if for any elements x, y, z ∈ X, if x is in relation with element y and y is in relation with element z, then x is in relation with element z.
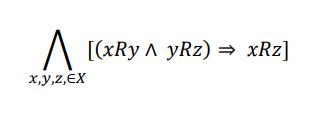
7. Connectedness
The relationship R defined on set X is connected if for any two elements x, y ∈ X, element x remains in relation with element y, or element y remains in relation with element x.
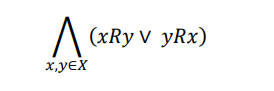
8. Equivalence relation
We call a relation equivalence if it is reflexive, symmetric, and transitive.